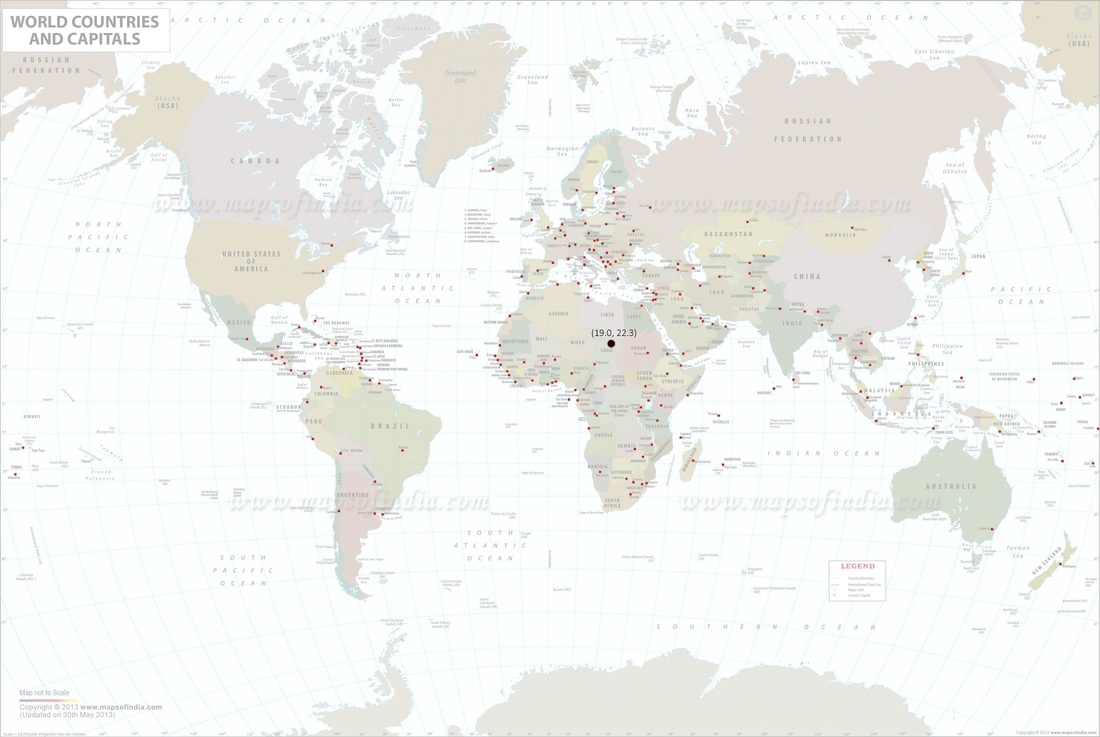
A thread on Reddit inspired me to figure out "What point on Earth is the geographical center of all the world capitals." Going into this, I first looked at a map of all the world capitals (as seen in the first image below, with all the red dots) and tried to make a guess. I estimated the center would be somewhere in the eastern Sahara Desert or near the Red Sea.
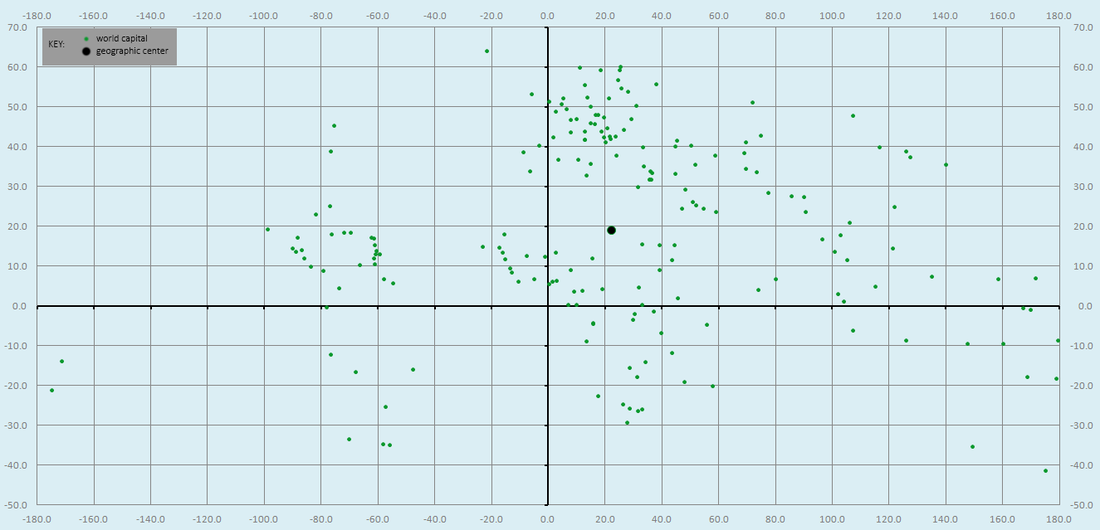
To solve this, I knew I'd have to gather all the capitals' latitude/longitude coordinates and translate them into a scatter plot and then find the center of that scatter plot. Already, that method is technically flawed because it doesn't allow for measuring distances across the International Date Line, however given the expanse of the Pacific Ocean I'm figuring that won't be a problem.
Once I'd gathered the coordinates, I realized I wasn't quite sure how to calculate the center of a scatter plot. My first gut thought was just to take the average of all the x-coordinates and the average of all the y-coordinates and then, BAM, you have a single "average coordinate." However that sounded too simple to me, so I opened up the question to my fellow mathletes on Facebook and Reddit and they eventually pointed me towards the following approach: "start by guessing a point in the scatter plot, calculate the straight-line distance to each data point, square those distances, and then minimize the sum of those squares via the Solver add-in in Excel which moves around the point you originally guessed." This is where things get weird. When I calculated the average coordinate via the former/simplistic method, I got [19.0, 22.3]; when I used the latter/mathematician-sounding method, I got.... [19.0, 22.3]. One would think that that would just go to show that there are two methods of getting at the same solution. However, my above-quoted friend (who I trust to know more about statistical analysis than myself) was baffled at how this happened, adding that he didn't expect it and didn't know why that happened. Anyways, when you plot that point on the map (as seen in the first image below, in the black dot) you get a location in north-central Chad, specifically the Ennedi-Ouest region - so I feel pretty good about my "eastern Sahara" estimate.
Before I declared that the final answer, I had to check against one last potential answer that probably wasn't what the original asker intended. Since the average radius of Earth is 3,959 miles, every national capital is exactly* that distance away from the center of the Earth. I use the asterisk because technically it's +/- 10 miles to account for variance in the Earth's radius as well as crust elevation differences (La Paz, Bolivia for example is 2.2 miles above sea level). So if the average distance from this central point in the Chadian desert to each national capital is greater than 3,959, then technically the closest point to each city would become the center of the Earth. As much as I would like this to be the case for the sake of trick questions, the average distance between the central point and each capital is 3,514 miles - 445 miles shorter than the distance to the center of the Earth.
To solve this, I knew I'd have to gather all the capitals' latitude/longitude coordinates and translate them into a scatter plot and then find the center of that scatter plot. Already, that method is technically flawed because it doesn't allow for measuring distances across the International Date Line, however given the expanse of the Pacific Ocean I'm figuring that won't be a problem.
Once I'd gathered the coordinates, I realized I wasn't quite sure how to calculate the center of a scatter plot. My first gut thought was just to take the average of all the x-coordinates and the average of all the y-coordinates and then, BAM, you have a single "average coordinate." However that sounded too simple to me, so I opened up the question to my fellow mathletes on Facebook and Reddit and they eventually pointed me towards the following approach: "start by guessing a point in the scatter plot, calculate the straight-line distance to each data point, square those distances, and then minimize the sum of those squares via the Solver add-in in Excel which moves around the point you originally guessed." This is where things get weird. When I calculated the average coordinate via the former/simplistic method, I got [19.0, 22.3]; when I used the latter/mathematician-sounding method, I got.... [19.0, 22.3]. One would think that that would just go to show that there are two methods of getting at the same solution. However, my above-quoted friend (who I trust to know more about statistical analysis than myself) was baffled at how this happened, adding that he didn't expect it and didn't know why that happened. Anyways, when you plot that point on the map (as seen in the first image below, in the black dot) you get a location in north-central Chad, specifically the Ennedi-Ouest region - so I feel pretty good about my "eastern Sahara" estimate.
Before I declared that the final answer, I had to check against one last potential answer that probably wasn't what the original asker intended. Since the average radius of Earth is 3,959 miles, every national capital is exactly* that distance away from the center of the Earth. I use the asterisk because technically it's +/- 10 miles to account for variance in the Earth's radius as well as crust elevation differences (La Paz, Bolivia for example is 2.2 miles above sea level). So if the average distance from this central point in the Chadian desert to each national capital is greater than 3,959, then technically the closest point to each city would become the center of the Earth. As much as I would like this to be the case for the sake of trick questions, the average distance between the central point and each capital is 3,514 miles - 445 miles shorter than the distance to the center of the Earth.
And here's the same image as above, but in its scatter-plot form:
 RSS Feed
RSS Feed
